FUNCIÓN DE TRANSFERENCIA (EXPLICACIÓN BREVE)

FUNCIÓN DE TRANSFERENCIA

En esta ocasión hablaremos de la función de transferencia a nivel general, para luego darle una aplicación en circuitos.
El concepto de función de transferencia es algo que encontraras continuamente en varios textos y cursos que te dispongas a realizar. Y no es para menos, pues la función de transferencia es una herramienta importantísima que nos permitirá analizar cómo se comportará un determinado proceso, bien sea industrial o académico, a lo largo del tiempo.

En pocas palabras una función de transferencia es una función matemática lineal que emplea la famosa herramienta matemática de la transformada de Laplace y permite representar el comportamiento dinámico y estacionario de cualquier sistema. Sin embargo vamos a detallar este concepto minuciosamente.

Sabemos que cuando nos encontramos en frente de algún proceso, sea cual sea, este proceso por lo general contará con actuadores y sensores. Los actuadores harán con que mis variables (presión, temperatura, nivel, humedad, velocidad, etc) comiencen a variar con el tiempo, mientras que los sensores se encargan de medir y mostrarme como dichas variables están cambiando con el tiempo.

Obviamente nosotros vamos a querer controlar estas variables del proceso, porque simplemente no vamos a dejar que estas variables evolucionen con el tiempo de la manera que ellas quieran. Por decir algo, si tenemos un horno, donde estamos cocinando galletas. No vamos a dejar que la variable temperatura suba a valores muy elevados, porque el resultado sería tener unas galletas totalmente quemadas. Es por eso que debemos controlar la temperatura para que esta se mantenga sobre una determinada zona y nos permita obtener una galletas perfectas!

Origen de la Función de Transferencia

Pero aquí llega el primer inconveniente. Para poder hacer los cálculos matemáticos de nuestros controladores, es de vital importancia, primero y antes que nada, conocer y entender cómo se comporta nuestro proceso. Y tenemos que hallar la forma de representar ese proceso que está en la industria en el Papel. Es decir encontrar alguna ecuación matemática que me permita modelar y simular el comportamiento real de mi proceso.

Ahí es donde tiene origen la función de transferencia. Si observamos los datos que nos entrega algún sensor de nuestro proceso, después de haber aplicado alguna perturbación (es decir después de prender los quemadores, después de abrir una válvula, etc) veremos que la variable comenzará a evolucionar en el tiempo hasta alcanzar otro estado donde se quedara estable, conocido en la literatura como el estado estacionario. Entonces de ese movimiento dinámico podemos clasificar el comportamiento del proceso en el tiempo de dos formas, como lo vemos en la siguiente figura:

En la zona dinámica el sistema va variando con el tiempo, y en la zona estacionaria, el sistema ya no depende más del tiempo, porque sin importar si el tiempo sigue creciendo, la variable se mantiene en el mismo valor.

Los físicos, matemáticos, químicos, necesitaban modelar los procesos industriales, es por eso que en base a estas respuestas dinámicas, se consiguen elaborar ecuaciones diferenciales que representan la evolución de las variables con el tiempo (Como ejemplo se muestra una ecuación diferencial de un reactor)

Ahora trabajar con este tipo de ecuaciones diferenciales puede llegar a ser un poco complicado, es por eso que aplicando el concepto de Tylor para linealizar aquellas ecuaciones diferenciales que fueran NO lineales y luego aplicando un herramienta conocida como la transformada de Laplace, podemos representar nuestro sistema que originalmente estaba en el tiempo en forma de ecuaciones diferenciales a representarlo en una nueva variable, llamada variable compleja “S” en forma de ecuaciones algebraicas.

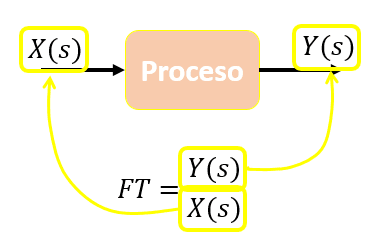
Asi surgen nuestra función de transferencia, las cuales relacionan la salida del sistema sobre la entrada. De esa manera puedo yo saber cómo se comporta mi sistema de una forma matemática y puedo posteriormente hacer los cálculos para un controlador.

Función de Transferencia de un Proceso

Si analizamos, veremos que las funciones de transferencia se componen de un numerador que es un polinomio y un denominador, que también es un polinomio. Y como todo polinomio tiene raíces, aquí aparece otro concepto que debemos tener claro.

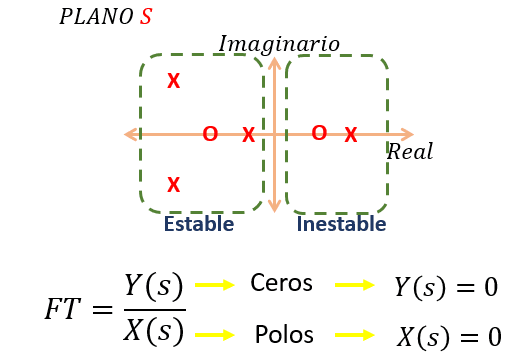
Cuando igualamos el polinomio del numerador a cero, vamos a obtener unas raíces que llamaremos como los “Ceros del Sistema” y haremos lo mismo con el polinomio del denominador, el cual igualaremos a cero y sus raíces se llamaran “Polos del Sistema”

Plano Complejo S y su Función de Transferencia

Los ceros y polos pueden ser graficados en el plano complejo “S” y aquí podremos determinar si una función de transferencia es estable o inestable. Simplemente con mirar la ubicación de los Polos del Sistema. Si algún polo del sistema se encuentra ubicado en el semiplano derecho del plano “S”, automáticamente sabremos que el sistema es Inestable. Si encontramos algún cero en esta zona, nuestro sistema NO será inestable, apenas tendrá un determinado comportamiento en su respuesta dinámica que analizaremos más adelante.

Como lo puedes evidenciar los polos y ceros de una función de transferencia caracterizan la forma y el comportamiento que tendrá un determinado sistema ante una eventual entrada de excitación.

Como Obtener una Función de Transferencia

Existen diferentes formas de obtener una función de transferencia:

1. Linealizando una Ecuación Diferencial y aplicando la transformada de Laplace.
2. Tomando datos de los sensores del proceso para aplicar posteriormente técnicas de identificación de sistemas.

Ambas formas de obtener una función de transferencias han sido explicadas en este canal, en el curso de análisis de sistemas. Por ejemplo puedes ver como obtener las funciones de transferencia de un sistema de llenado de tanques aplicando el primer método.

Accede al siguiente link donde encontraras un vídeo explicativo sobre el concepto físico de esta temática.

Vídeo explicativo sobre función de transferencia.

Si te gusta la temática de este blog por favor conviértete en seguidor, comparte con demás compañeros y deja un comentario. 

EXPLICACIÓN DEL MÉTODO DE RUFFINI (FACTORIZACION DE EXPRESIONES DE GRADO SUPERIOR)

 MÉTODO DE RUFFINI

Con la regla de Ruffini, solamente se obtienen las soluciones enteras. Si la ecuación tiene soluciones complejas o reales, éste método no es válido.

Veremos que para obtener las soluciones de la ecuación, previamente hay que factorizar, por lo que con el mismo ejemplo explicaremos ambos conceptos.

Vamos a resolver un ejemplo explicando paso por paso.

Tenemos la siguiente ecuación:

1 – Identificamos los coeficientes de cada término, que son los números que van delante de la incógnita. Para la ecuación anterior, los represento en verde para identificarlos:

2 – Trazamos dos líneas perpendiculares de esta forma:

3 – Colocamos los coeficientes ordenados por su grado de mayor o menor:

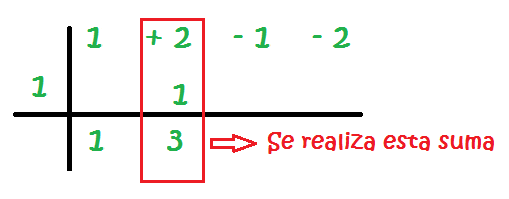
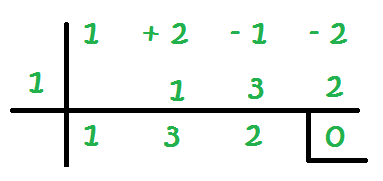
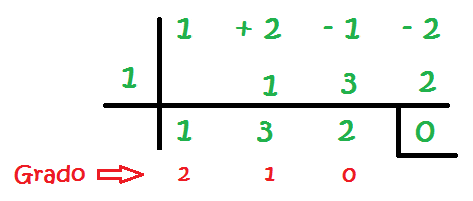
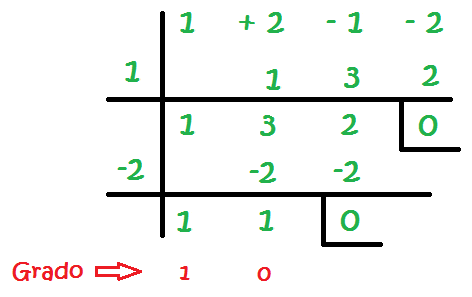
En la regla de Ruffini, el grado va disminuyendo de 1 en 1 y cada grado tiene su lugar. Por ejemplo si no tuviérmos ningún término que tenga x², en el lugar del grado 2, se colocaría un 0.

Los números que hemos escrito hasta ahora en el método de Ruffini, es equivalente a escribir la ecuación, es decir:

4 – Ahora escribimos un número a la izquierda de la línea vertical. Más adelante explicaremos qué número colocar aquí y por qué. De momento, empezamos con el 1.

Ese número corresponde al número (a) del binomio x – a:

En este caso, escribir ahí un 1, significa el binomio (x – 1) en el método de Ruffini

5 – Empezamos a ejecutar el método. El primer hueco de la segunda fila, siempre se deja libre:

7 – Se multiplica el número de la izquierda por el resultado de la suma de la primera columna. El resultado se coloca en el hueco de la segunda columna:

8 – Se realiza la suma de la segunda columna:

9 – Se multiplica el número de la izquierda por el resultado de la suma de la segunda columna. El resultado se coloca en el hueco de la tercera columna:

10 – Así sucesivamente hasta completar todas las columnas:

El objetivo es que en la última columna tengamos un 0. Esta es la explicación de qué número colocar a la izquierda de la línea:

Si no tenemos un cero, tendríamos que probar con otro número a la izquierda de la línea vertical y reiniciar el proceso.

Una vez hemos obtenido un cero al final, vamos a ver qué significa lo que tenemos hasta aquí:

Lo que nos ha quedado en la última fila es otra ecuación, pero ahora, el número que está a la izquierda del 0, tiene grado 0 y  éste va aumentando de 1 en 1 hacia la izquierda. En este caso, nos queda lo equivalente a tener esta ecuación:

Y como hemos visto antes, el 1 a la izquierda de la línea vertical significaba:

Lo que quiere decir que lo que tenemos hasta ahora es el producto de esas dos ecuaciones, que es igual a la ecuación original:

11 – Con la fila que nos ha quedado, volvemos a empezar. Empezamos probando con el 1:

12 – Igual que antes, vamos multiplicando con el resultado de sumar en cada columna:

Al final tenemos un 6, y lo que queremos es tener un cero. Por tanto, debemos seguir probando, con -1, con 2, con -2… hasta encontrar el número que nos haga tener un cero en la última columna.

El número que nos hace tener un 0 al final es el -2:

¿Y ahora que hacemos? ¿Cómo sabemos que hemos terminado?

El mayor grado de la última fila es 1, por tanto hemos terminado:

El resultado de la factorización de la ecuacuón por el método de Ruffini es el producto de la última fila y de los números que están a la izquierda de la línea vertical, pero expresados en forma de ecuación:

Por tanto, nuestra ecuación será:

Hasta aquí hemos factorizado la ecuación. Ahora vamos a resolverla:

1 – Igualamos a 0, tal y como estaba en un principio

2 – Recuerda que cuando una multiplicación de dos o más factores tiene como resultado 0, quiere decir que uno de los factores es 0, ya que cualquier valor multiplicado por 0 es 0. Por tanto, cualquier factor podría ser 0.

Nos quedan tres ecuaciones de primer grado para despejar, de donde obtenemos las tres soluciones (ya que es una ecuación de tercer grado):

Soluciones: -1, -2 y 1