LEYES DE KEPLER

Introducción

Johannes Kepler fue un hombre profundamente religioso que escogió las herramientas del pujante método científico para construir una visión del Cosmos que reflejara la armonía divina. Con sus tres leyes del movimiento planetario dio elegante expresión matemática a las observaciones de Tycho Brahe, reafirmó el heliocentrismo copernicano y allanó el camino a la síntesis newtoniana. Como tantos otros pioneros de la frontera científica, coqueteó con disciplinas ahora consideras supersticiones; en su caso, la astrología, de la cual llegó a convertirse en experto reclamado por reyes y príncipes. Ni el favor de los poderosos ni su devoción le sustrajeron, no obstante, de las terribles consecuencias de la guerras religiosas que asolaban Europa

Elementos básicos de una elipse.

Una elipse se define como el conjunto de puntos (x,y) cuya suma de distancia a dos puntos distintos prefijos (focos) es constante. Como tal es una generalización del círculo, el cual es una elipse especial que tiene ambos focos en la misma posición. La forma de una elipse cual alargada es, está representada por su excentricidad, que para la elipse puede ser cualquier número que va desde cero hasta muy cerca de uno, pero siempre menor. La elipse está formada por dos ejes perpendiculares entre si, el semieje mayor a y el semieje menor b. Según la definición de la elipse tenemos que: 

Aplicamos esta definición para el caso específico donde las dos distancias son iguales

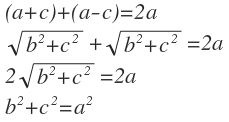
Ecuación de la elipse en coordenadas cartesianas

Vamos a encontrar la ecuación de la elipse, para ello nos tomamos dos puntos, el B y P en los cuales se forman los triángulos f´Bf y f´Pf, en el que sabemos que la suma de las distancias es 2a

Principales elementos de la elipse centrada en el origen

Tomando la definición básica de elipse para el triángulo de color verde f´P + Pf = 2a, aplicando tenemos:

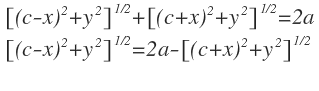
Elevando ambos miembros al cuadrado tenemos

Simplificando y ordenando los términos de la ecuación precedente

Elevamos nuevamente al cuadrado miembro a miembro para eliminar la raíz:

Amplificando la ecuación a2 = b2 + c2 en la expresión anterior:

Dividiendo miembro a miembro por a2b2 y simplificando tenemos la ecuación canónica de la elipse centrada en el origen.

Ecuación de la elipse en coordenadas polares

Otra representación útil y común de la elipse es en términos de coordenadas polares (r, Φ), tomando como origen a uno de los focos  se tiene entonces que:

Entonces a partir del esquema anterior tenemos que:

Sustituimos estas expresiones en la ecuación de la elipse en coordenadas cartesianas y se obtiene:

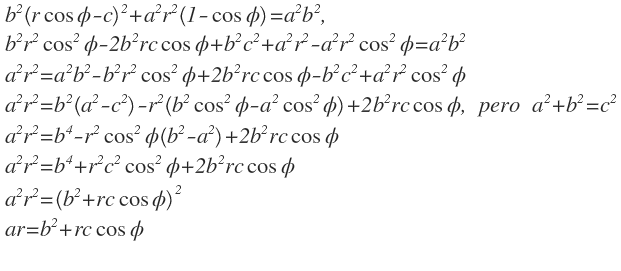
Extrayendo raíz, se deduce que:

Veamos algunas propiedades adicionales de las elipses. Coloquemos el origen en uno de los focos y sea r1 la distancia mínima (perigeo) y r2 la distancia máxima (apogeo) entre el origen y la elipse. Se tiene que:

Excentricidad

La excentricidad es una propiedad fundamental para el estudio de las órbitas de los planetas, pues ello describen elipse de distinta excentricidad, algunos tan cercano a cero que parecen que fueran circular. Desde la antiguedad hasta los tiempos de Kepler se pensó que esto era así, sin embargo, el autor demostraría matemáticamente y consecuente a los datos que eran forma elíptica.

La excentricidad ε (épsilon) de una elipse es la razón entre su semidistancia focal (longitud del segmento que parte del centro de la elipse y acaba en uno de sus focos), denominada por la letra c, y su semieje mayor. Su valor se encuentra entre cero y uno. (Tomado de Wikipedia)

La excentricidad indica la forma de una elipse; una elipse será más redondeada cuanto más se aproxime su excentricidad al valor cero.5 La designación tradicional de la excentricidad es la letra griega ε llamada épsilon.

Leyes de Kepler

Primera ley

Los planetas describen órbitas elípticas estando el sol en uno de sus focos.

Imagen que muestra los planetas con sus correspondientes excentricidades y donde el sol se ubica en el foco de esas elipses.

Segunda ley

Los planetas se mueven con velocidad areolar constante. Es decir, el vector posición r de cada planeta con respecto al Sol barre áreas iguales en tiempos iguales. Se puede demostrar que el momento angular es constante lo que nos lleva a las siguientes conclusiones:

• Las órbitas son planas y estables.
• Se recorren siempre en el mismo sentido.
• La fuerza que mueve los planetas es central.

Imagen 1: Muestra la como la fuerza de atracción gravitatoria es una fuerza central siempre perpendicular a la velocidad y al vector desplazamiento.

Imagen 2: Muestra que el área es del triángulo formado posición y desplazamiento.

Imagen 3: Muestra de una manera gráfica la segunda ley, donde las áreas barridas por el radio vector son iguales en tiempos iguales, es decir al A1 es igual a A2.

Se puede demostrar que la segunda ley de Kepler es una consecuencia de la conservación de la cantidad de movimiento angular. Sea el planeta Mp que va una velocidad V girando de manera elíptica en torno al sol que está en uno de sus focos. Para ello se considera que el sol no se mueve, así la fuerza de atracción ejercida por el sol es una fuerza central siempre a lo largo del radio vector dirigido hacia el sol. Claramente el torque neto como siempre es perpendicular vale cero.

la imagen 2 muestra que en un intervalo de tiempo dt, el radio vector r  barre el área dA, que es igual a la mitad del área formado por r y dr.

 

donde L y Mp son constantes, lo anterior muestra que el radio vector desde el sol a cualquier planeta barre áreas iguales en tiempos iguales.

Tercera ley de Kepler

La tercera ley se puede deducir a partir de la ley de gravitación de Newton, en la cual se considera una fuerza de tipo inversa cuadrática donde Mp es la masa del sol en una órbita circular.

Como la excentricidad de los planetas es bastante pequeña, podemos asumir como aproximación que las órbitas de los planetas son circulares, entonces, a partir de la tercer ley de Kepler, podemos encontrar una expresión para la magnitud de la fuerza gravitacional.

Para órbitas elípticas la ecuación anterior también es válido si se sustituye r con la longitud a del semieje mayor.

Si asumimos que, en primera aproximación, las órbitas de los planetas son circulares, entonces, a partir de la tercera ley de Kepler, podemos encontrar una expresión para la magnitud de la fuerza gravitacional.

Como el semieje mayor de una órbita circular es su radio, esta ecuación es válida tanto para órbitas circulares como para elípticas. También debe tener presente que el valor de la constante depende del planeta o astro que esté en el foco de la elipse que describe el cuerpo que gira. En el caso tierra luna, debe ir la masa de la tierra.