MOVIMIENTO ARMÓNICO SIMPLE

Decimos que una partícula o sistema tiene movimiento armónico simple (m.a.s) cuando vibra bajo la acción de fuerzas restauradoras que son proporcionales a la distancia respecto a la posición de equilibrio. Decimos, entonces, que dicho cuerpo es un oscilador armónico. En este apartado estudiaremos:

• El concepto de vibración u oscilación y sus tipos
• La definición del m.a.s. y sus características principales
• Las magnitudes que lo definen
• Su gráfica de posición
• Algunos casos típicos de m.a.s. en tu día a día

Adicionalmente, es posible que tengas interés en profundizar en el comportamiento del m.a.s. Te aconsejamos que visites:

• Cinemática del movimiento armónico simple
• Dinámica del movimiento armónico simple

Vamos allá.

Oscilaciones y Vibraciones

¿Sabrías decir qué tienen en común un péndulo, el latido de tu corazón, la membrana de los altavoces de tu equipo de música o el mecanismo de un reloj? Se podría decir, en un sentido figurado, que todos ellos generan oscilaciones o vibraciones que nos marcan el ritmo. En este apartado vamos a explicar las características qué tienen en común todos estos movimientos y para ello vamos a presentar el movimiento armónico simple (m.a.s.) también conocido como movimiento vibratorio armónico simple (m.v.a.s.).

Para entender el movimiento armónico simple es importante entender el concepto de oscilación o vibración. Los cuerpos oscilan o vibran cuando se apartan de su posición de equilibrio establMuelle vertical en movimiento armónico simple

Decimos que un cuerpo oscila o vibra cuando se mueve de forma periódica en torno a una posición de equilibrio debido al efecto de fuerzas restauradoras. Las mágnitudes características de un movimiento oscilatorio o vibratorio son:

1. Periodo (T): El tiempo que tarda de cumplirse una oscilación completa.  Su unidad de medida en el Sistema Internacional es el segundo (s)
2. Frecuencia (f): Se trata del número de veces que se repite una oscilación en un segundo. Su unidad de medida en el Sistema Internacional es el hertzio (Hz)

En el caso de la bola del ejemplo anterior, el periodo es el tiempo que tarda esta en volver a pasar por el mismo punto en igual sentido. La frecuencia es el número de veces en un segundo en que la bola pasa por el mismo punto en igual sentido.

El periodo y la frecuencia son magnitudes inversas:

f=1/T

Con esto tenemos que 1 Hz = 1 s-1

Aunque el concepto de vibración es el mismo que el de oscilación, en ocasiones se emplea el término vibración para designar una oscilación muy rápida o de alta frecuencia.

Tipos de vibraciones

Existen dos tipos de vibraciones u oscilaciones atendiendo a las fuerzas que actúan:

1. Oscilaciones libres: Cuando sobre el cuerpo no actúan fuerzas disipativas. El cuerpo no se detiene, oscila indefinidamente, al no haber una fuerza que contrarreste el efecto de la fuerza restauradora  
2. Oscilaciones amortiguadas: Cuando actúan fuerzas disipativas (como por ejemplo la fuerza de rozamiento o de fricción) que acaban por hacer que las oscilaciones desaparezcan. El cuerpo acabará retornando a la posición de equilibrio

El Movimiento Armónico Simple: Características

Cuando las fuerzas restauradoras que actúan sobre la partícula son proporcionales a la distancia al punto de equilibrio, decimos que se produce un movimiento armónico simple (m.a.s), también conocido como movimiento vibratorio armónico simple (m.v.a.s.). En general, dichas fuerzas restauradoras siguen la ley de Hooke:

F→=−k⋅x→

Una partícula o sistema tiene movimiento armónico simple (m.a.s.) cuando vibra bajo la acción de fuerzas restauradoras que son proporcionales a la distancia respecto a la posición de equilibrio.

La bola del experimenta y aprende anterior es un movimiento armónico simple pues, como puede observarse, la fuerza restauradora, en rojo, es proporcional a la distancia al punto de equilibrio.

Características del movimiento armónico simple:

1. Vibratorio: El cuerpo oscila en torno a una posición de equilibrio siempre en el mismo plano
2. Periódico: El movimiento se repite cada cierto tiempo denominado periodo (T). Es decir, el cuerpo vuelve a tener las mismas magnitudes cinemáticas y dinámicas cada T segundos
3. Se describe mediante una función sinusoidal (seno o coseno indistintamente)
   x=A⋅cos(ω⋅t+φ0)
   x=A⋅sin(ω⋅t+φ0)

A la partícula o sistema que se mueve según un movimiento armónico simple se les denomina oscilador armónico.

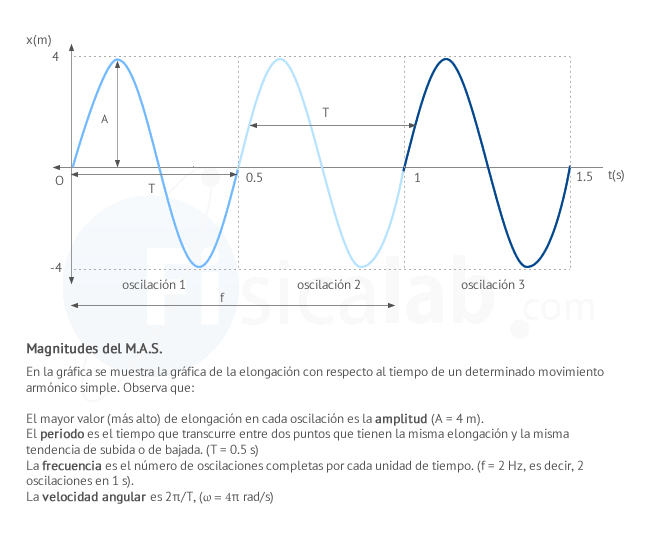
Magnitudes del movimiento armónico simple

1. Elongación, x: Representa la posición de la partícula que oscila en función del tiempo y es la separación del cuerpo de la posición de equilibrio. Su unidad de medidas en el Sistema Internacional es el metro (m)
2. Amplitud, A: Elongación máxima. Su unidad de medidas en el Sistema Internacional es el metro (m).
3. Frecuencia. f: El número de oscilaciones o vibraciones que se producen en un segundo. Su unidad de medida en el Sistema Internacional es el Hertzio (Hz). 1 Hz = 1 oscilación / segundo = 1 s-1.
4. Periodo, T: El tiempo que tarda en cumplirse una oscilación completa. Es la inversa de la frecuencia T = 1/f . Su unidad de medida en el Sistema Internacional es el segundo (s).
5. Fase, φ : La fase del movimiento en cualquier instante. Corresponde con el valor φ=ω⋅t+φ0. Se trata del ángulo que representa el estado de vibración del cuerpo en un instante determinado. Su unidad de medida en el Sistema Internacional es el radián (rad). Cuando se produce una oscilación completa, la fase aumenta en 2·π radianes y el cuerpo vuelve a su posición (elongación) x inicial. Esto es debido a que cos(φ)=cos(φ+2⋅π) 
6. Fase inicial, φ0 : Se trata del ángulo que representa el estado inicial de vibración, es decir, la elongación x del cuerpo en el instante t = 0. Su unidad de medida en el Sistema Internacional es el radián (rad)
7. Frecuencia angular, velocidad angular o pulsación, ω : Representa la velocidad de cambio de la fase del movimiento. Se trata del número de periodos comprendidos en 2·π segundos. Su unidad de medida en el sistema internacional es el radián por segundo ( rad/s ). Su relación con el período y la frecuencia es ω=2⋅πT=2⋅π⋅f 

Gráfica de posición en el movimiento armónico simple (m.a.s.)

No es casualidad que el movimiento armónico simple se denomine, precisamente, armónico. También las funciones seno y coseno suelen denominarse funciones armónicas. 

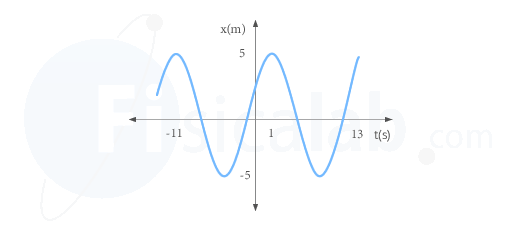
La gráfica de la elongación del movimiento armónico simple es la de una función sinusoidal cuya variable independiente es el tiempo.

Experimenta y Aprende

0

5

10

15

20

25

30

0

5

10

-5

-10

A (m) = 4.00

ω (rad/s) = 0.40

φ0 (rad) = 0.00

Magnitudes del M.A.S.

t (s)

x (m)

Magnitudes m.a.s.

La gráfica representa la elongación de una partícula que se mueve según un M.A.S. a lo largo del tiempo.

x(t) = A · sen (ω·t+φ0)

Desliza los valores de las magnitudes de amplitud (A), velocidad angular (ω) y la fase inicial (φ0) y observa que ocurre en la gráfica.

• Si aumentas A aumentarás la distancia entre los extremos de la trayectoria.
• Si aumentas ω y por tanto la frecuencia, disminuyes el periodo (disminuyes el tiempo en que se tarda en realizar una oscilación completa).
• Si aumentas la φ0, desplazas la posición inicial de la partícula.

Algunos casos de movimiento armónico simple

Es frecuente estudiar algunos elementos que se comportan como osciladores armónicos para entender las propiedades y características del m.a.s. con mayor profundidad. En este tema vamos a estudiar:

• El m.a.s. en muelles
• El m.a.s. en péndulos
• El movimiento armónico simple en el movimiento circular uniforme

Recuerdo de trigonometría...

Existen algunas relaciones trigonométricas que es importante que recuerdes y que te serán útiles cuando resuelvas ejercicios de este tema:

cos(α)=sin(α+π/2)

sin(α)=cos(α−π/2)

sin(α±π)=−sin(α)

cos(α±π)=−cos(α)

Ejemplo

La siguiente gráfica representa la elongación en función del tiempo de un cuerpo que se comporta según un movimiento armónico simple:

Determina la amplitud máxima, el periodo, la frecuencia, la frecuencia angular y la fase inicial del movimiento.